50. The cut number
Vasylko wrote a number which
is multiple of d on
a scrap of paper. His smaller brother Dmytro cut the number into k parts. Vasylko decided
to restore the number that he wrote. He remembered only number d. But there was a problem.
It is possible to make many numbers which are multiple of d.
How many numbers multiple of d can make Vasylko? He
must use all parts to make a number.
Input. First line contains
two integers d and k (1
≤ k < 9, 1 ≤ d ≤ 100). The parts of the number
are given in the next k lines. The
number of digits in each part does not exceed 10.
Output. Print the amount of
different numbers, divisible by d.
|
Sample input |
Sample output |
|
5 3 13 85 45 |
4 |
SOLUTION
combinatorics - permutations
Algorithm analysis
Put the numbers of all parts into the array. Consider all
possible gluing of the available parts. Such full
search is possible, since k
< 9 and
there will be no more than 9! different
gluings. For each number obtained by
gluing, check is it
divisible by d.
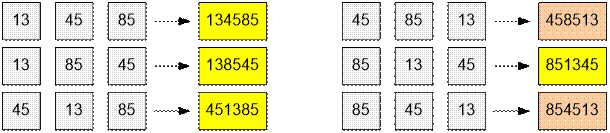
Example
Consider
all possible gluings of three
parts 13, 85 and 45. For each number obtained, check whether it is divisible by
d = 5.
Algorithm realization
Function f returns the value of 10k, where k is the number of digits in number n.
long long f(long long n)
{
long long res = 1;
while (n > 0)
{
res *= 10;
n /= 10;
}
return res;
}
The main part of the program. Store the numbers written on the parts of the paper into array v.
scanf("%d %d", &d, &k);
for (c = i = 0; i < k; i++)
{
scanf("%lld", &value);
v.push_back(value);
}
Sort the
numbers written on the parts.
sort(v.begin(),
v.end());
Iterate
over all possible permutations of parts using next_permutation. In the
variable value, calculate the
remainder of dividing the glued number by d.
do
{
for (i = value =
0; i < k; i++)
Append v[i] to
the right of the value.
value = (value * f(v[i]) + v[i]) % d;
If the resulting glued number value is divisible by d, increase counter c by 1.
if (value % d ==
0) c++;
} while (next_permutation(v.begin(), v.end()));
Print the answer.
printf("%d\n", c);